Note
Go to the end to download the full example code.
1. empymod: 1D VTI resistivity#
The code empymod is an open-source code which can model CSEM responses for
a layered medium including VTI electrical anisotropy, see emsig.xyz.
Content:
Full-space VTI model for a finite length, finite strength, rotated bipole.
Layered model for a deep water model with a point dipole source.
import emg3d
import empymod
import numpy as np
import matplotlib.pyplot as plt
1. Full-space VTI model for a finite length, finite strength, rotated bipole#
In order to shorten the build-time of the gallery we use a coarse model.
Set coarse_model = False to obtain a result of higher accuracy.
coarse_model = True
Survey and model parameters#
# Receiver coordinates
if coarse_model:
x = (np.arange(256))*20-2550
else:
x = (np.arange(1025))*5-2560
rx = np.repeat([x, ], np.size(x), axis=0)
ry = rx.transpose()
frx, fry = rx.ravel(), ry.ravel()
rz = -400.0
azimuth = 33
elevation = 18
# Source coordinates, frequency, and strength
source = emg3d.TxElectricDipole(
coordinates=[-50, 50, -30, 30, -320., -280.], # [x1, x2, y1, y2, z1, z2]
strength=np.pi, # A
)
frequency = 1.1 # Hz
# Model parameters
h_res = 1. # Horizontal resistivity
aniso = np.sqrt(2.) # Anisotropy
v_res = h_res*aniso**2 # Vertical resistivity
1.a Regular VTI case#
empymod#
Note: The coordinate system of empymod is positive z down, for emg3d it is positive z up. We have to switch therefore src_z, rec_z, and elevation.
# Collect common input for empymod.
inp = {
'src': np.r_[source.coordinates[:4], -source.coordinates[4:]],
'depth': [],
'res': h_res,
'aniso': aniso,
'strength': source.strength,
'srcpts': 5,
'freqtime': frequency,
'htarg': {'pts_per_dec': -1},
}
# Compute
epm = empymod.bipole(
rec=[frx, fry, -rz, azimuth, -elevation], verb=3, **inp
).reshape(np.shape(rx))
:: empymod START :: v2.3.1
depth [m] :
res [Ohm.m] : 1
aniso [-] : 1.41421
epermH [-] : 1
epermV [-] : 1
mpermH [-] : 1
mpermV [-] : 1
> MODEL IS A FULLSPACE
direct field : Comp. in wavenumber domain
frequency [Hz] : 1.1
Hankel : DLF (Fast Hankel Transform)
> Filter : key_201_2009
> DLF type : Lagged Convolution
Loop over : Frequencies
Source(s) : 1 bipole(s)
> intpts : 5
> length [m] : 123.288
> strength[A] : 3.14159
> x_c [m] : 0
> y_c [m] : 0
> z_c [m] : 300
> azimuth [°] : 30.9638
> dip [°] : -18.9318
Receiver(s) : 65536 dipole(s)
> x [m] : -2550 - 2550 : 65536 [min-max; #]
> y [m] : -2550 - 2550 : 65536 [min-max; #]
> z [m] : 400
> azimuth [°] : 33
> dip [°] : -18
Required ab's : 11 12 13 21 22 23 31 32 33
:: empymod END; runtime = 0:00:00.396927 :: 45 kernel call(s)
emg3d#
if coarse_model:
min_width_limits = 40
stretching = [1.045, 1.045]
else:
min_width_limits = 20
stretching = [1.03, 1.045]
# Create stretched grid
grid = emg3d.construct_mesh(
frequency=frequency,
properties=h_res,
center=source.center,
domain=([-2500, 2500], [-2500, 2500], [-2900, 2100]),
min_width_limits=min_width_limits,
stretching=stretching,
lambda_from_center=True,
lambda_factor=0.8,
center_on_edge=False,
)
grid
:: emg3d START :: 15:38:16 :: v1.8.3
MG-cycle : 'F' sslsolver : False
semicoarsening : False [0] tol : 1e-06
linerelaxation : False [0] maxit : 50
nu_{i,1,c,2} : 0, 2, 1, 2 verb : 4
Original grid : 80 x 80 x 80 => 512,000 cells
Coarsest grid : 5 x 5 x 5 => 125 cells
Coarsest level : 4 ; 4 ; 4
[hh:mm:ss] rel. error [abs. error, last/prev] l s
h_
2h_ \ /
4h_ \ /\ /
8h_ \ /\ / \ /
16h_ \/\/ \/ \/
[15:38:17] 3.578e-02 after 1 F-cycles [4.601e-05, 0.036] 0 0
[15:38:18] 3.734e-03 after 2 F-cycles [4.801e-06, 0.104] 0 0
[15:38:19] 4.985e-04 after 3 F-cycles [6.411e-07, 0.134] 0 0
[15:38:20] 7.463e-05 after 4 F-cycles [9.597e-08, 0.150] 0 0
[15:38:21] 1.198e-05 after 5 F-cycles [1.541e-08, 0.161] 0 0
[15:38:22] 2.044e-06 after 6 F-cycles [2.629e-09, 0.171] 0 0
[15:38:23] 3.953e-07 after 7 F-cycles [5.083e-10, 0.193] 0 0
> CONVERGED
> MG cycles : 7
> Final rel. error : 3.953e-07
:: emg3d END :: 15:38:23 :: runtime = 0:00:07
Plot function#
def plot(epm, e3d, title, vmin, vmax):
# Start figure.
a_kwargs = {'cmap': "viridis", 'vmin': vmin, 'vmax': vmax,
'shading': 'nearest'}
e_kwargs = {'cmap': plt.get_cmap("RdBu_r", 8),
'vmin': -2, 'vmax': 2, 'shading': 'nearest'}
fig, axs = plt.subplots(2, 3, figsize=(10, 5.5), sharex=True, sharey=True,
subplot_kw={'box_aspect': 1})
((ax1, ax2, ax3), (ax4, ax5, ax6)) = axs
x3 = x/1000 # km
# Plot Re(data)
ax1.set_title(r"(a) |Re(empymod)|")
cf0 = ax1.pcolormesh(x3, x3, np.log10(epm.real.amp()), **a_kwargs)
ax2.set_title(r"(b) |Re(emg3d)|")
ax2.pcolormesh(x3, x3, np.log10(e3d.real.amp()), **a_kwargs)
ax3.set_title(r"(c) Error real part")
rel_error = 100*np.abs((epm.real - e3d.real) / epm.real)
cf2 = ax3.pcolormesh(x3, x3, np.log10(rel_error), **e_kwargs)
# Plot Im(data)
ax4.set_title(r"(d) |Im(empymod)|")
ax4.pcolormesh(x3, x3, np.log10(epm.imag.amp()), **a_kwargs)
ax5.set_title(r"(e) |Im(emg3d)|")
ax5.pcolormesh(x3, x3, np.log10(e3d.imag.amp()), **a_kwargs)
ax6.set_title(r"(f) Error imaginary part")
rel_error = 100*np.abs((epm.imag - e3d.imag) / epm.imag)
ax6.pcolormesh(x3, x3, np.log10(rel_error), **e_kwargs)
# Colorbars
unit = "(V/m)" if "E" in title else "(A/m)"
fig.colorbar(cf0, ax=axs[0, :], label=r"$\log_{10}$ Amplitude "+unit)
cbar = fig.colorbar(cf2, ax=axs[1, :], label=r"Relative Error")
cbar.set_ticks([-2, -1, 0, 1, 2])
cbar.ax.set_yticklabels([r"$0.01\,\%$", r"$0.1\,\%$", r"$1\,\%$",
r"$10\,\%$", r"$100\,\%$"])
ax1.set_xlim(min(x3), max(x3))
ax1.set_ylim(min(x3), max(x3))
# Axis label
fig.text(0.4, 0.05, "Inline Offset (km)", fontsize=14)
fig.text(0.05, 0.3, "Crossline Offset (km)", rotation=90, fontsize=14)
fig.suptitle(title, y=1, fontsize=20)
print(f"- Source: {source}")
print(f"- Frequency: {frequency} Hz")
rtype = "Electric" if "E" in title else "Magnetic"
print(f"- {rtype} receivers: z={rz} m; θ={azimuth}°, φ={elevation}°")
Plot#
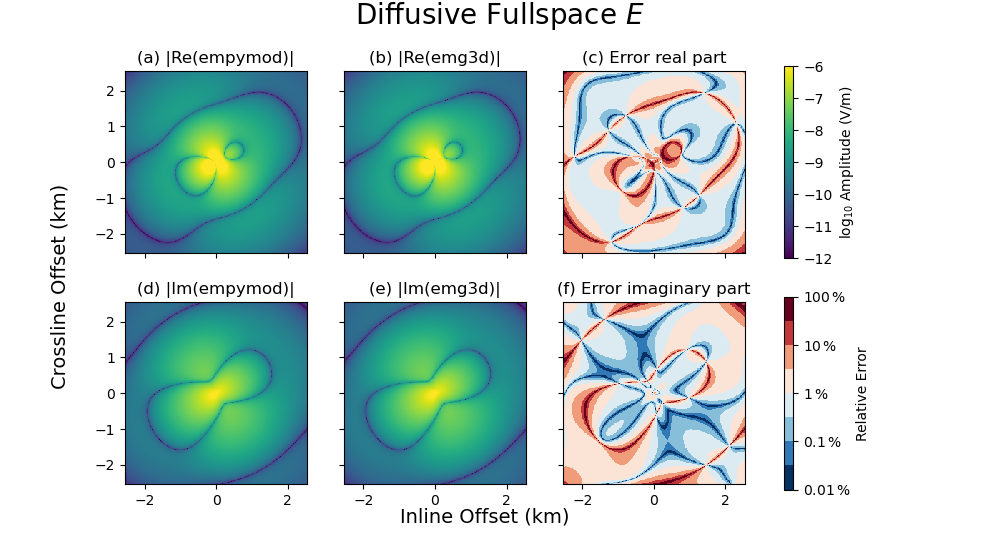
- Source: TxElectricDipole: 3.1 A;
e1={-50.0; -30.0; -320.0} m; e2={50.0; 30.0; -280.0} m
- Frequency: 1.1 Hz
- Electric receivers: z=-400.0 m; θ=33°, φ=18°
2. Layered model for a deep water model with a point dipole source#
Survey and model parameters#
# Receiver coordinates
if coarse_model:
x = (np.arange(256))*20-2550
else:
x = (np.arange(1025))*5-2560
rx = np.repeat([x, ], np.size(x), axis=0)
ry = rx.transpose()
frx, fry = rx.ravel(), ry.ravel()
rz = -950.0
azimuth = 30
elevation = 5
# Source coordinates and frequency
source = emg3d.TxElectricDipole(coordinates=[0, 0, -900, 0, 0])
frequency = 1.0 # Hz
# Model parameters
h_res = [1, 50, 1, 0.3, 1e12] # Horizontal resistivity
aniso = np.sqrt([2, 2, 2, 1, 1]) # Anisotropy
v_res = h_res*aniso**2 # Vertical resistivity
depth = np.array([-2200, -2000, -1000, 0]) # Layer boundaries
empymod#
:: empymod START :: v2.3.1
depth [m] : -2200 -2000 -1000 0
res [Ohm.m] : 1 50 1 0.3 1E+12
aniso [-] : 1.41421 1.41421 1.41421 1 1
epermH [-] : 1 1 1 1 1
epermV [-] : 1 1 1 1 1
mpermH [-] : 1 1 1 1 1
mpermV [-] : 1 1 1 1 1
direct field : Comp. in wavenumber domain
frequency [Hz] : 1
Hankel : DLF (Fast Hankel Transform)
> Filter : key_201_2009
> DLF type : Lagged Convolution
Loop over : Frequencies
Source(s) : 1 dipole(s)
> x [m] : 0
> y [m] : 0
> z [m] : -900
> azimuth [°] : 0
> dip [°] : 0
Receiver(s) : 65536 dipole(s)
> x [m] : -2550 - 2550 : 65536 [min-max; #]
> y [m] : -2550 - 2550 : 65536 [min-max; #]
> z [m] : -950
> azimuth [°] : 30
> dip [°] : 5
Required ab's : 11 21 31
:: empymod END; runtime = 0:00:00.035018 :: 3 kernel call(s)
emg3d#
if coarse_model:
min_width_limits = 40
else:
min_width_limits = 20
# Create stretched grid
grid = emg3d.construct_mesh(
frequency=frequency,
properties=[h_res[3], h_res[0]],
center=source.center,
domain=([-2500, 2500], [-2500, 2500], None),
vector=(None, None, -2200 + np.arange(111)*20),
min_width_limits=min_width_limits,
stretching=[1.1, 1.5],
center_on_edge=False,
)
grid
# Create the model: horizontal resistivity
res_x_full = h_res[0]*np.ones(grid.n_cells) # Background
res_x_full[grid.cell_centers[:, 2] >= depth[0]] = h_res[1] # Target
res_x_full[grid.cell_centers[:, 2] >= depth[1]] = h_res[2] # Overburden
res_x_full[grid.cell_centers[:, 2] >= depth[2]] = h_res[3] # Water
res_x_full[grid.cell_centers[:, 2] >= depth[3]] = h_res[4] # Air
# Create the model: vertical resistivity
res_z_full = v_res[0]*np.ones(grid.n_cells) # Background
res_z_full[grid.cell_centers[:, 2] >= depth[0]] = v_res[1]
res_z_full[grid.cell_centers[:, 2] >= depth[1]] = v_res[2]
res_z_full[grid.cell_centers[:, 2] >= depth[2]] = v_res[3]
res_z_full[grid.cell_centers[:, 2] >= depth[3]] = v_res[4]
# Get the model
model = emg3d.Model(
grid, property_x=res_x_full, property_z=res_z_full,
mapping='Resistivity')
:: emg3d START :: 15:38:25 :: v1.8.3
MG-cycle : 'F' sslsolver : 'bicgstab'
semicoarsening : True [1 2 3] tol : 1e-06
linerelaxation : True [4 5 6] maxit : 50 (3)
nu_{i,1,c,2} : 0, 2, 1, 2 verb : 4
Original grid : 64 x 64 x 160 => 655,360 cells
Coarsest grid : 2 x 2 x 5 => 20 cells
Coarsest level : 5 ; 5 ; 5
[hh:mm:ss] rel. error solver MG l s
h_
2h_ \ /
4h_ \ /\ /
8h_ \ /\ / \ /
16h_ \ /\ / \ / \ /
32h_ \/\/ \/ \/ \/
[15:38:29] 2.609e-03 after 1 F-cycles 4 1
[15:38:33] 6.118e-05 after 2 F-cycles 5 2
[15:38:37] 1.494e-04 after 3 F-cycles 6 3
[15:38:42] 5.038e-06 after 4 F-cycles 4 1
[15:38:46] 1.933e-06 after 5 F-cycles 5 2
[15:38:50] 1.344e-05 after 6 F-cycles 6 3
[15:38:50] 3.922e-06 after 1 bicgstab-cycles
[15:38:54] 1.480e-07 after 7 F-cycles 4 1
[15:38:59] 6.793e-07 after 8 F-cycles 5 2
[15:38:59] 6.771e-07 after 2 bicgstab-cycles
> CONVERGED
> Solver steps : 2
> MG prec. steps : 8
> Final rel. error : 6.771e-07
:: emg3d END :: 15:38:59 :: runtime = 0:00:34
Plot#
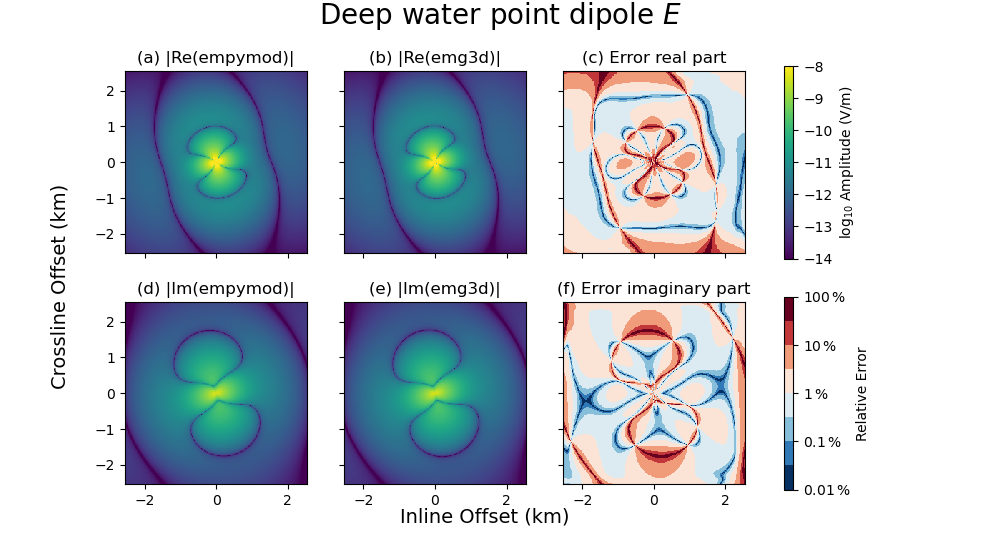
- Source: TxElectricDipole: 1.0 A;
center={0.0; 0.0; -900.0} m; θ=0.0°, φ=0.0°; l=1.0 m
- Frequency: 1.0 Hz
- Electric receivers: z=-950.0 m; θ=30°, φ=5°
Total running time of the script: (0 minutes 44.267 seconds)
Estimated memory usage: 453 MB